The relationship between Fourier domain and space domain

Gray scale images are considered as being composed by superposition of two-dimensional (2D) sine waves. The spatial frequency or Fourier domain representation of an image gives the amplitude (intensity) and phase (where does the sine wave start) of individual sine wave components as a function of direction and spatial frequency (w). The discrete Fourier transformation converts spatial domain data into frequency domain data (e.g. B-G ii to i or H to I below), while the inverse discrete Fourier transformation (the real part of the transform) converts frequency domain data back to spatial domain. The Fourier domain comprises of complex numbers, and during visualization the absolute value of these complex values is shown. The ‘1’ here therefore means amplitude of 1 and phase of zero (the phase is the argument of the complex number). For better visualization the origin is placed (both for space and Fourier domain images) into the center of the images below.

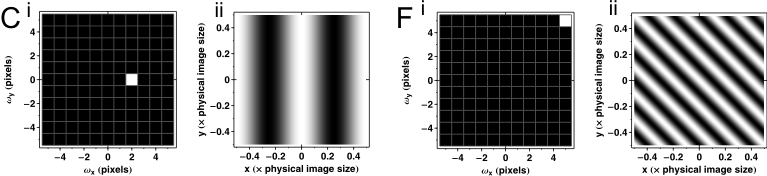
(A) The origin of the Fourier domain corresponds to the mean intensity of the image.
(B-D) Single pixels of the Fourier domain correspond to different spatial sine waves; the frequency of the sine wave (i.e. how many times does the sine repeats across the image) equals to the absolute coordinate of the ‘1’ pixel in the Fourier domain.
(F) The angle of the sine waves correspond to the position (angle) of the ‘1’ pixel compared to the origin of the Fourier domain.
(G) When placing the origin in the middle, the 128 pixels are scaled between -64 and 63, so the maximal spatial frequency is reached only at -64, resulting a line by line black and white striped spatial image

The relationship between Fourier domain and space domain. (A-G) Fourier domain images were generated as 128´128 pixel blank (0) images with Mathematica 5.2, and the indicated pixel was set to 1. (A) The origin of the Fourier domain corresponds to the mean intensity of the image. (i) The middle 11´11 pixel region of the 128´128 Fourier domain (ii) is shown. (ii) Space domain, the uniform gray value represents 1/128 intensity corresponding to the single pixel set to 1 in (i & ii). (B-F) The middle 11´11 pixel region of the Fourier domain (i) and the space domain (ii) are shown. (G) The 128128 Fourier domain (i) and the space domain (ii) are shown. (B-G ii) the amplitude (the maximal intensity corresponding to white) in the spatial images is 1/128. 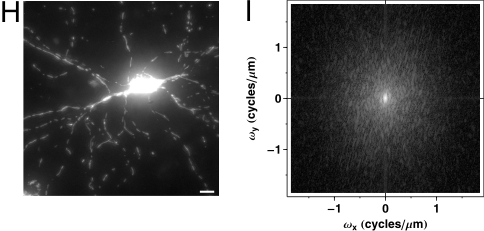(H) Maximum intensity projected wide-field fluorescence micrograph of a mito-DsRed2 expressing neuron, a 512´512 image, scaled at 0.27 mm/pixel. Scale bar, 10 mm (I) The Fourier domain of image (H), shown in a logarithmic scale for better visibility.

Fourier domain image representations were generated by Mathematica (Wolfram Research).